[통계학] 5시간 만에 끝나는 통계학 기초강의_메타코드M_확률과 확률변수(확률 변수~공분산과 상관계수)

급하게 말고 차근차근..!

통계 기초 이론 3강 확률과 확률변수의 4-7 소강의 이다.

5시간만에 끝난다니 얼마나 매력적인가..

 

3강 확률과 확률변수는 7개의 소강의, 총 1시간 20분 길이로 되어 있다.

 

3.4 확률변수/이산확률변수/연속확률변수

 

확률변수

 

1. 확률변수  
   - 표본공간에서 정의된 실수값 함수
     - 실수가 아니면 확률분포함수를 정의할 수 없음 (그래프를 못그립니다..!)
   - 일정 확률을 가지고 발생하는 사건에 수치를 부여한 것
      why? 계산을 할 수 있기 때문
   - 변수가 어떤 값을 취하는지가 확률적으로 결정된다  
     - 통계적 규칙성은 있다고 봄

  -> 간단히 말해 사건을 실수 값에 매핑하는 것!  
  
2. 확률분포  
   - 확률변수의 값과, 확률을 대응시켜  
     표, 그래프, 함수로 표현한 것

 

 -> 확률변수의 설명서!
 정규분포, 베르누이 분포, T 분포, 이항분포 등을 보고 데이터가 이런 모형이고 성질을 가지고 있을 것이라 추측, 모델링이 가능!(노이즈를 감안하더라도)

나아가, Random Variable(이데아)를 통해 Data(현실)를 생성 가능!

* very 철학적..

 

이산/연속확률변수

1. 이산확률변수
   - 이산표본공간에서 정의된 확률변수의 값이 유한 혹은 countably infinite
   - 확률질량함수(probability mass function) : 이산확률변수 X의 값 x1, ..., xn의 각 확률을 대응

 

2. 연속확률변수
   - 특정 구간 내의 모든 값을 취하는 확률변수
   - 확률변수의 값이 무한개이며 셀 수 없음
   - 확률밀도함수(probability density function)
     확률변수 X가 어떤 구간 [l, u]의 모든 값을 취하고 이 구간에서의 함수 f(x)

 

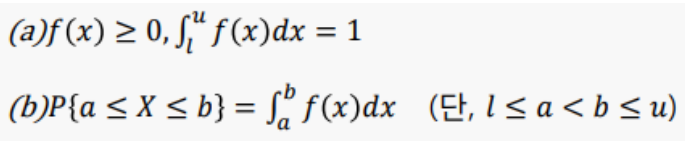
연속확률변수의 특징

 구간의 적분을 통해서 계산

P(X=x) = 0 특정되는 순간 0이 됨. why? 취할 수 있는 값이 무한개이기 때문에 확률이 무한대가 되므로, 0으로 정의.

구간을 적분한 넓이가 확률!!!!

데이터의 분포를 확인하기 위해 사용함.

 

* 누적분포함수CDF(cumulative density function) : 확률을 확인하기 위해 확률밀도함수(pdf)를 적분함.

  - y 값이 0, 특정 함수가 특정 값 이하일 확률 P(X ≤ x)

CDF의 일반적인 모양

슬슬 멘붕이 오는데 한마디로

누적분포함수(CDF)를 미분하면 연속확률변수(PDF)가 됨.

3.5 기대값

기대값

 

1. 기대값(expected value) : 확률변수의 모든 값의 평균

   - 이산확률변수
     - 확률변수의 값이 x1, ...이고 X=xi일 확률이 f(xi)일 때,

 

 

단순히 매핑하여 각각 곱한 뒤 다 더하면 됨.

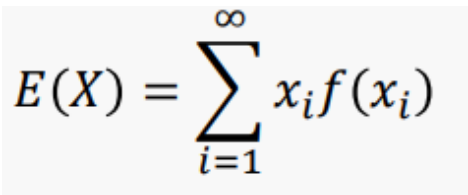
- 연속확률변수
  - 확률변수 X가 어떤 구간 [l, u]의 모든 값을 취하고
    X의 확률밀도함수가 f(x)일 때,

RV의 특정 값과 확률밀도함수를 곱한 뒤 적분을 취함.
    

 

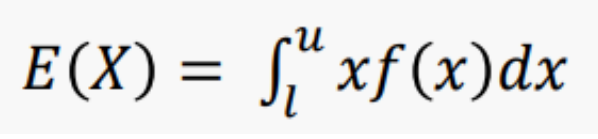
[기대값의 성질] - 반드시 알고 있어야 함!

기대값의 성질 (a, b는 상수이고 X, Y는 확률변수)

 

E(a) = a

- random성이 없기 때문에 그대로 상수 값이 나옴

 

E(aX) = a · E(X)

- a에 대해서는 RV 영향이 없기 때문에 여기서도 그대로 나옴!

 

E(X ± b) - E(X) ± b

- b 또한 상수이기 때문에 그대로 나옴

 

E(aX ± b) = a · E(X) ± b

- 위의 식을 응용하면 상수 부분은 독립적으로 적용 가능

 

E[c1g1(X) + c2g2(X)] = c1E[g1(X)] + c

- g1와 g2는 확률변수(함수) 이므로 영향을 받아 나오게 됨.

 

적용 예시)

기대값 : 우리나라 평균 남성 키 E(X)
A 나라가 우리나라 남성 키보다 2cm 크더라 ->
E(X±b) = E(X)± b
A 나라 키 평균 = 우리나라 키 평균 ± 2

 

 

3.6 분산과 표준편차

 

분산과 표준편차

 

 

1. 분산

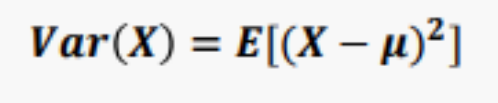
   E : 기대값

   X : 확률변수

   μ : X의 기댓값 E(x)

   편차 제곱의 평균, 분산을 구하는 방식과 동일함.


   1. 이산확률변수
    

   2. 연속확률변수

   * 주의 - 적분을 취하는 이유 : f(x)는 확률변수의 값이 아님

     pdf-> cdf의 미분값이므로 확률값을 가지고 있기 때문에 확률의 정의에 맞지 않음(합이 1이 안된다..!!!)
  
2. 표준편차

 

분산과 표준편차의 성질

   1. 분산과 표준편차의 연산

   - 더했는데 달라지지 않은 이유 : 편차 제곱을 합하면 b가 자기들끼리 소거됨

 - 분산은 a가 제곱이 되서 나오고, 편차는 루트가 씌워지기 때문에 a가 그대로 나옴!

  - 분산은 a는 제곱이 되서 나오나 b는 사라짐. 마찬가지로 편차는 a가 그대로 나오고 b는 소거되어 없어짐.

 

정규분포를 따르면 b만큼 움직암. 그러나 모양은 안바뀜.

-> 중심은 바뀌었으나 모양(분산)은 바뀌지 않음

3.7 공분산과 상관계수

공분산과 상관계수

1. 공분산과 상관계수

   공분산(Sx)/Sx · Sy

 

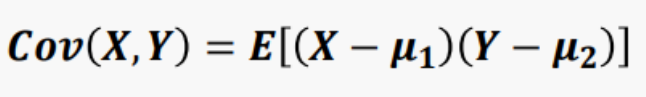
2. 공분산과 상관계수의 성질

 

- ac 만큼 스케일이 변화되어 출력

- 각각의 곱만 곱해지고, 상수는 사라지게 됨
- 비교를 해주기 위해 ac는 사라지고 부호에만 영향을 주게 됨

  - ac > 0 (a>0, c>0), (a<0, c<0)

  - ac < 0 (a>0, c<0), (a<0, c>0)

3. 두 확률변수 합의 분산
- Var(X + Y) = Var(X) + Var(Y) + 2Cov(X,Y)

  * 각각의 분산만큼 더해주고 + 두 분산의 관계만큼 더해주면 됨.

- Var(X – Y) = Var(X) + Var(Y) – 2Cov(X,Y)

  * 각각의 분산만큼 더해주고 - 두 분산의 관계만큼 빼주면 됨.

 

E(X+Y) = E(x) + E(Y)

* 기대값은 그대로

특이사항

** 독립가정일 경우 : 2 Cov(X,Y)는 사라지게 됨. (관계가 없기 때문...!!)

---

이외에 매 통계 강의 뒤에 예제가 있어서 풀어볼 수 있고, 풀이도 알려주셔서 바로 적용해볼 수 있다.

통계 기초 강의 맛보기는 유튜브에서, 강의는 메타코드M 사이트에서 들을 수 있다.

데이터 분야에서는 어떻게 쓰이는지에 대해서도 알려주셔서 이해가 쉬웠다.

---

https://youtu.be/r7jTwciTdXo?feature=shared

 

https://mcode.co.kr/video/list2?viewMode=view&idx=45

메타코드M