통계 기초 이론 4강 이산확률분포다.

4강 이산확률분포는 약 20분여 길이로 되어 있다.

4.1 이산확률분포 : 이항분포
데이터 분석 실무에 적합한 효율적인 분포 위주로 배우기 때문에, 본 강의에서는
이항, 베르누이, 포아송 분포 중심으로 배우게 된다.
이외의 분포도 알 수 있다.

베르누이 분포는 이항 분포의 어머니라고 볼 수 있다.
1. 베르누이 시행 (trial) : 사상이 두 개뿐인 시행(성공 or 실패)
- 각 시행에서 성공확률과 실패확률의 합은 1
- 각 시행은 서로 독립
- 베르누이 시행을 n 번 독립 시행했을 때의 확률 변수 x의 분포는 이항분포이다.
-> 이항분포 : 베르누이 시행을 반복했을 때의 분포!

- 이 때, 확률변수 X의 평균(기대값) : p
- 확률변수 X의 분산 : p(1-p)
* 확률변수값*대응하는 확률값 의 총합
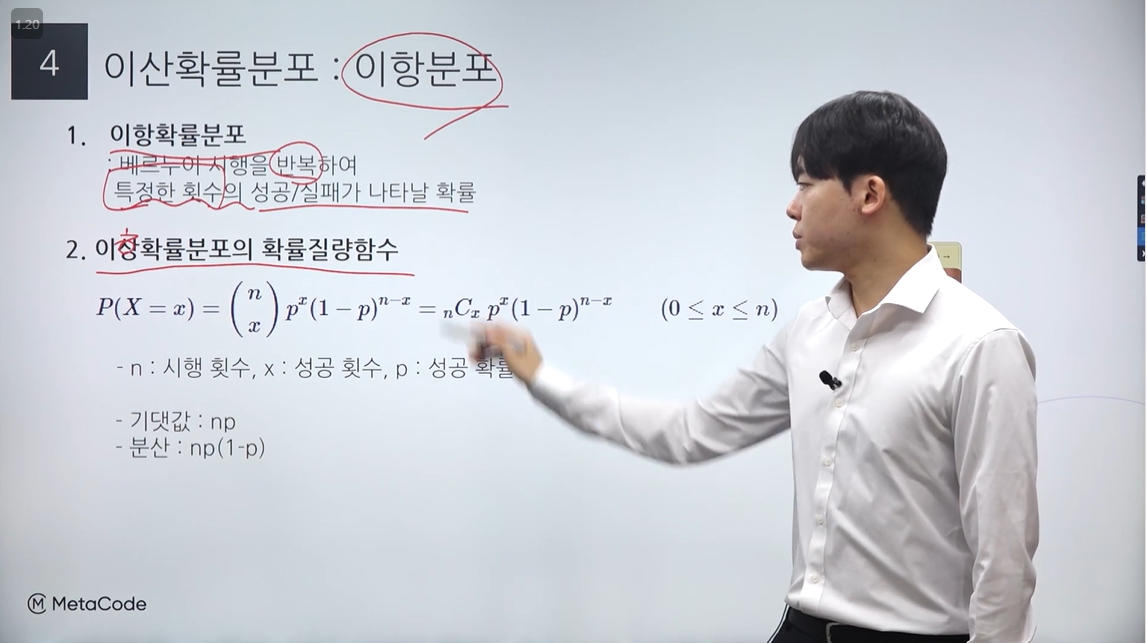
2. 이항확률분포 : 베르누이 시행을 반복하여 특정한 횟수의 성공/실패가 나타날 확률
3. 이항확률분포의 확률질량함수(pmf)
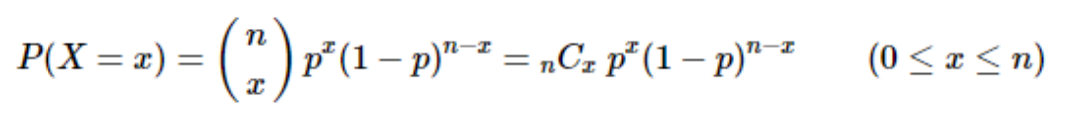
- n ; 시행횟수, x : 성공 횟수(확률변수 실제 값), p : 성공 확률
- 기댓값 : np
- 분산 : np(1-p)
베르누이 시행을 n 번 반복했기 때문에 n을 곱해주면 된다!
X~B(n, p)

1. 포아송분포
- 단위시간, 단위공간 내 발생하는 사건의 횟수를 확률변수 X라고 할 때, X 는 λ 를 모수로 갖는 포아송 분포를 따름
- 발생빈도가 낮은 사건의 단위 당 발생 수
예시) 1분당, 1㎥당 발생하는 사건의 횟수
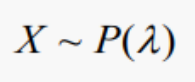
2. 포아송분포의 확률함수

- X : 데이터
- 기댓값 : λ
- 분산 : λ
여기에 있는 기댓값과 분산을 구하는 공식 또한 유사한데, 결국 풀어서 계산하면 λ 만 나오게 된다.
4.2 이산확률분포 : 예제

1. 확률변수 X가 베르누이분포를 따를 때, X의 분산이 p(1-p)임을 보여라
| X | 0 | 1 |
| P | 1-P | P |
μ
=0*(1-P) + (1*P)
= P
분산 공식 : E(X- μ)^2
= E(X^2) - μ^2
= P - P^2
=P(1-P)
2. 주사위를 5번 던질 때, 4 이상의 눈이 두 번 나올 확률은?
n = 5
x = 2
p = 1/2
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
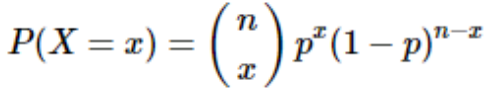
위 식에 대입해보면 결과가 나온다.
3. 동전을 5번 던질 때, 앞면이 나온 횟수를 X라고 하자. 이 때, X의 기댓값과 분산은?
n = 5
X~B(5, 1/2)
p = 1/2
기댓값 = np
분산 = np(1-p)
4. 1000명의 보험가입자가 있을 때, 한 해에 보험금을 청구할 확률이 1/2000이다.
어떤 해에 보험금이 3회 청구될 확률은?
-> 포아송 분포 (단위시간 : 한 해)
X~P(λ)
x = 3
λ = 1000*1/2000 = 0.5
한 해에 0.5명이 보험금을 청구함

위 공식에 대입하면 결과가 나온다.
이외에 매 통계 강의 뒤에 예제가 있어서 풀어볼 수 있고, 풀이도 알려주셔서 바로 적용해볼 수 있다.
통계 기초 강의 맛보기는 유튜브에서, 강의는 메타코드M 사이트에서 들을 수 있다.
데이터 분야에서는 어떻게 쓰이는지에 대해서도 알려주셔서 이해가 쉬웠다.
https://youtu.be/r7jTwciTdXo?feature=shared
https://mcode.co.kr/video/list2?viewMode=view&idx=45
메타코드M
빅데이터 , AI 강의 플랫폼 & IT 현직자 모임 플랫폼ㅣ메타코드 커뮤니티 일원이 되시기 바랍니다.
mcode.co.kr
'배움' 카테고리의 다른 글
| [가벼운 학습지] 가벼운 학습지 중국어!! 도전해보자! 2주차 (0) | 2024.02.04 |
|---|---|
| [통계학] 5시간 만에 끝나는 통계학 기초강의_메타코드M_연속확률분포 (0) | 2024.02.03 |
| [독후감] 청소부 밥 (0) | 2024.01.29 |
| [통계학] 5시간 만에 끝나는 통계학 기초강의_메타코드M_확률과 확률변수(확률 변수~공분산과 상관계수) (0) | 2024.01.27 |
| [가벼운 학습지] 가벼운 학습지 중국어!! 도전해보자! 1주차 (0) | 2024.01.27 |