앞으로 두 강 남았다...!!! 열심히 달리자.
통계 기초 이론 5강 이산확률분포다.

5강 연속확률분포는 총 대략 1시간 길이로 되어 있다.
핵심 부분이고 종류도 다양해서 그런 것 같다!

5.1 연속확률분포 : Uniform Distribution

2. 확률밀도함수 (PDF)

확률밀도 함수 그래프

* 확률값이 아니기 때문에 확률을 알기 위해서는 적분을 통해 cdf를 구해 알아야 함.
- 기댓값 : (a+b)/2
- 분산 : (b_a)^2/12
5.2 연속확률분포 : 정규분포

1. 정규분포(가우스분포)
- 연속확률분포 중 가장 널리 사용(거의 default 값)
- 표본을 통한 통계적 추정 및 가설검정이론의 기본 *가장 많이 본 분포..!
- 샘플 사이즈가 클 경우, 대부분 정규분포를 따름.
2. 확률밀도함수
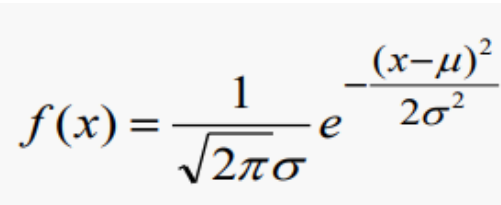
꽤 복잡해 보임.. 따라서 다른 확률변수와 비교할 수 있게 표준화함
X~N(0,1) : 0과 1 시아의 값으로 표준화시킴.
그럼에도 불구하고 확률을 계산하기 부담스럽기 때문에 확률분포표를 제공함.
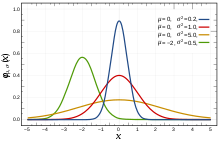
정규분포의 특징
1. Bell Shaped : 평균을 중심으로 좌우 대칭의 종모양이다.
2. 평균 = 중앙 = 최빈값
3. 평균에 의해 분포의 위치가 결정 X~N( μ , σ² )
4. 표준편차에 의해 분포 모양이 결정
- 표준편차가 크면 평평한 곡선이 됨
5. 확률변수 X가 어느 구간에 속할 확률은 그 구간과 분포함수로 이루어진 면적값이다.
6. 이항분포와 포아송분포는 일정조건이 만족될 때 정규분포로 근사가 가능하다.
- 이항분포 : np > 5 and n(1-p) > 5
- 포아송분포 : λ > 5
5.3 연속확률분포 : 표본분포

* 매우 중요! : 추정과 검정을 할 때, 표본분포가 반드시 들어감.
1. 표본분포 (sampling distribution)
모집단에서 일정한 크기로 뽑을 수 있는 표본을 모두 뽑았을 때, 그 모든 표본의 통계량의 확률분포
-> 표본 추출을 여러 번 진행! 그에 따른 여러 개의 통계량을 모아서 분포를 확인
2. 표본평균의 평균과 표준편차
X1, ..., Xn 이 모평균 μ, 모표준편차 σ인 모집단으로부터의 확률표본 (i, i, d)일 때,
표본평균은
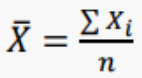
- 기대값 :
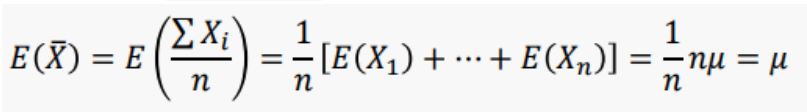
- 분산 :
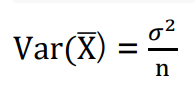
* 통계 데이터는 원 데이터보다 밀집된 경향을 보이기 때문에 일반적으로 분산이 원 데이터의 분산보다 작을 수 있다.
중심극한정리(CLT)
평균이 μ, 표준편차 σ인 임의의 모집단으로부터 크기 n인 표본에서의 표본평균은 n이 크면 근사적으로 평균이 μ이고 분산이 σ²/n인 정규분포를 따름
->모집단이 정규분포라면 표본평균은 표본 개수와 상관없이 항상 정규분포를 따른다.
5.4 연속확률분포 : 카이제곱 분포

1. 카이제곱( χ2 )분포
- 표본분산과 관련된 분포(통계량 관련!)
- 확률변수 Z1, ..., Zk 가 각각 표준정규분포를 따르고 독립일 때 그들의 제곱합은 자유도가 k인 카이제곱분포 χ2(k)를 따름.
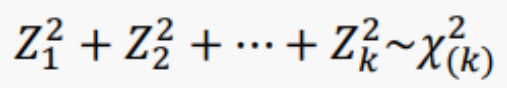
*자유도 k 하나만 있으면 구할 수 있음(포아송 분포와 유사)
표본분산을 알고 모분산을 추정할 때 사용하는 분포
(표본의 크기가 클수록 치우침이 적어짐 - 정규 분포에 근사할 수 있음)
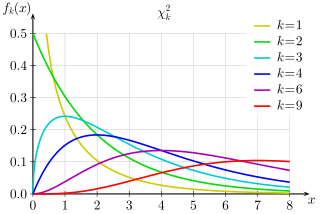
카이제곱 분포의 특징
1. 단봉분포
2. 오른쪽에 꼬리를 가짐(positive skewed)
3. 항상 양수값을 가짐
- 표본분산과 관련되어 있기 때문!
4. 자유도가 커지면 정규분포에 가까워짐
5. 모분산 추정 및 검정에 활용됨
6. 적합성, 동질성, 독립성 검정 등에 사용
- 범주형 자료 검정시 : 혈액형, MBTI 등
5.5.1 연속확률분포 : t분포

1. t분포
- X의 분포가 정규분포일 때, 표분평균의 분포에서 모집단의 표준편차를 모를 경우, 모표준편차 대신 표본표준편차를 사용
- t 분포는 자유도에 의해 모양이 결정됨!
Z ~N(0,1), V~ χ2(k) 이고 Z와 V는 서로 독립일 때,
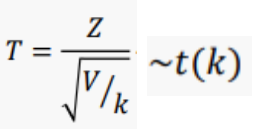
X1, ..., Xn ~ N ( μ , σ² )일 때,
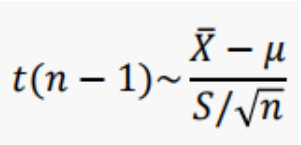
위의 식에서 기존 표본평균분포 공식을 기억한다면,
μ : 표본평균의 기댓값
σ²/n : 표본평균의 분산
σ/ √n : 표본평균의 표준편차
을 생각할 때
모수에 대한 표준편차 σ 를 모르기 때문에 표본표준편차인 S를 집어넣음
그러면 자유도가 n-1인 t 분포를 따른다.
t분포의 특성
1. t분포는 정규분포보다 넓게 퍼져 있고 꼬리 부분이 더 평평함
2. Bell shaped
3. 표본크기가 커질수록 분포가 중심부근에서 점점 더 뾰족해짐
- 표본 크기가 30 이상이 되면 정규분포에 근사
4. 주로 모평균 추정 혹은 모평균차이에 대한 추정 시 사용
모표준편차를 모를 때 t 분포를 사용함.
5. 표본 크기가 30 이상일 경우에는 표준정규분포, 미만일 때는 t 분포이다.
5.5.2 연속확률분포 : F분포

1. F 분포
F 분포는 두 정규 모집단의 분산을 비교하는 추론에 사용
V1과 V2는 각각 자유도 k1, k2인 카이제곱분포를 따르는 독립인 확률변수일 때,
V1 ~ χ2(k1), V2 ~ χ2(k2)
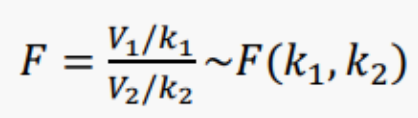
통계량을 사용할 경우,
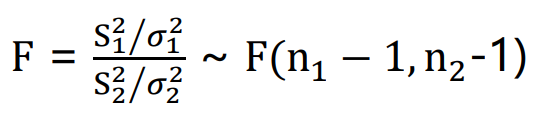
데이터를 통해 표준편차를 계산할 수 있다면, 위와 같이 F 분포를 구할 수 있음.
n1 : V1의 자유도
n2 : V2의 자유도
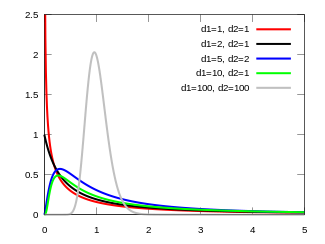
* 회귀 분석, ANOVA 분석 시 매우 유용한 분포
이번 강의는 통계 분석 시 많이 사용하는 연속확률변수의 통계 분포들에 대해 설명해 주셨는데,
확실히 기초이다 보니 간략하게만 언급한 부분이 없잖아 있다.
향후, 더 자세한 심화 버전으로 강의도 나온다고 하니, 그 내용을 기대하며 헷갈리지 않게 오늘 배운 것들을 잘 정리해야겠다.
이외에 매 통계 강의 뒤에 예제가 있어서 풀어볼 수 있고, 풀이도 알려주셔서 바로 적용해 볼 수 있다.
통계 기초 강의 맛보기는 유튜브에서, 강의는 메타코드M 사이트에서 들을 수 있다.
데이터 분야에서는 어떻게 쓰이는지에 대해서도 알려주셔서 이해가 쉬웠다.
https://youtu.be/r7jTwciTdXo?feature=shared
https://mcode.co.kr/video/list2?viewMode=view&idx=45
메타코드M
빅데이터 , AI 강의 플랫폼 & IT 현직자 모임 플랫폼ㅣ메타코드 커뮤니티 일원이 되시기 바랍니다.
mcode.co.kr
'배움' 카테고리의 다른 글
| [통계학] 5시간 만에 끝나는 통계학 기초강의_메타코드M_통계적 추정 (0) | 2024.02.04 |
|---|---|
| [가벼운 학습지] 가벼운 학습지 중국어!! 도전해보자! 2주차 (0) | 2024.02.04 |
| [통계학] 5시간 만에 끝나는 통계학 기초강의_메타코드M_이산확률분포 (0) | 2024.01.31 |
| [독후감] 청소부 밥 (0) | 2024.01.29 |
| [통계학] 5시간 만에 끝나는 통계학 기초강의_메타코드M_확률과 확률변수(확률 변수~공분산과 상관계수) (0) | 2024.01.27 |