통계학 기초 강의
통계 기초 이론 6강 통계적 추정이다.

6강 통계적 추정은 약 30분 길이로 되어 있다.
통계적 추정은 빅데이터 분석기사에서도 꽤 중요한 내용으로 나왔던 것으로 기억한다..!
6.1 통계적 추정
통계 inference의 꽃.

2. 통계적 추정의 종류
1) 점추정 : 모수의 단일한 값으로 추측하는 방식
- 신뢰도를 나타낼 수 없음
예) 대한민국 국민의 키 평균은 150cm이다!
2) 구간 추정 : 모수를 포함한다고 추정되는 구간을 구하는 방식
- 신뢰도를 나타낼 수 있음
예) 대한민국 국민의 키 평균은 148~152cm 사이에 있을 것이다!
통계적 추정의 기준
1. 불편성 (Unbiasedness) : 모수의 추정량( θ ^)의 기댓값이 모수( θ )가 되는 성질
- 편향이 없는 성질, E( θ ^) = θ
- n-1로 나누어 주는 이유
2. 유효성 (Efficiency) : 추정량이 불편추정량이고 분산이 다른 추정량에 비해 가장 작은 분산을 갖는 성질
- 추정량 또한 확률변수로써 narrow한 분산을 가질 수록 좋음
3. 일치성 (Consistency) : 표본 크기가 커질 수록 추정량이 모수에 수렴하는 성질
4. 충분성 (Sufficiency) : 모수에 대해 가능한 많은 표본정보를 내포하는 성질
-> 위 네가지 성질은 수리 통계학에 의해 엄밀하게 공식적으로 하나하나 체크한다.
6.2 통계적 추정 : 점추정

1. 표준오차 (Standard Error) : 통계량의 표준편차 (𝜎/√n)
- 표본크기가 클 수록 작아짐
- 추정량의 표준편차가 작을 수록 좋음
2. 점 추정량
1) 모평균 : 표본평균
2) 모분산 : 표본분산
3) 모표준편차 : 표본표준편차
4) 모비율 : 표본비율
점 추정은 그렇게 많이 사용되지 않으니 빠르게 구간추정으로 넘어가보자.
6.3 통계적 추정 : 구간추정

1. 구간추정 : 표본에서 얻어지는 정보를 이용하여 모수가 속할 것으로 기대되는 범위(신뢰구간)를 택하는 과정
- 통계적 추정은 일반적으로 신뢰구간의 추정을 활용
- 모수 𝜃 대하여 P(a < 𝜃 < b) = 1 - 𝛼 일 때, 구간 (a,b)을 모수 𝜃 대한 100(1- 𝛼)% 신뢰구간이라고 한다.
2. 신뢰구간 : 모수를 포함할 것으로 추정한 구간
3. 신뢰수준 : 신뢰구간이 모수를 포함할 확률 ( 1 - 𝛼 )
* 𝛼 : 오차율
- 동일한 표본추출을 통해 구한 신뢰구간들 중 100 x ( 1- 𝛼 ) %는 모수를 포함
예) 95% 신뢰수준이다 : 100개의 신뢰구간 중 95개는 모수를 포함하고 있다.
6.4 통계적 추정 : 모평균의 구간추정
모평균의 구간 추정은 시나리오를 나누어야 한다!

1. 모분산을 아는 경우
가정) 모분산을 안다.
모집단의 평균이 𝜇, 분산이 𝜎2인 정규분포
Z통계량을 사용
표준 정규분포
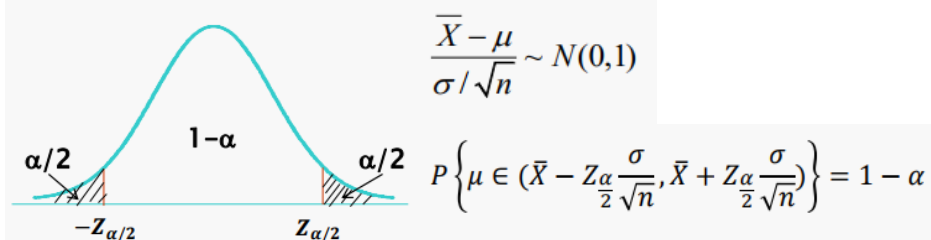
표준화를 진행시켜주어야 함.
-> 특정 확률 변수(X_)에 기대값( 𝜇 )을 빼주고, 그 확률변수의 STD (𝜎/√n) 로 나눠주면 된다.
구간을 추정하기 위해서는 신뢰수준을 설정해야 함.
신뢰 수준을 설정한 뒤, P(Z≤z) = 0.05(예시) 에 대한 z 값을 구해야 함.
how? 표준정규분포표를 보면 알 수 있음
- 90% 신뢰구간( 𝛼 =0.1) : Z0.05 = - 1.64 / Z0.95 - 1.64
- 95% 신뢰구간( 𝛼 =0.05) : Z0.025 = - 1.96
- 99% 신뢰구간( 𝛼 =0.01) : Z0.005 = - 2.57

2. 모분산을 모르는 경우(좀 더 일반적)
가정) 모분산을 모른다.
모집단의 평균이 𝜇, 분산이 𝜎^2인 정규분포
t통계량을 사용
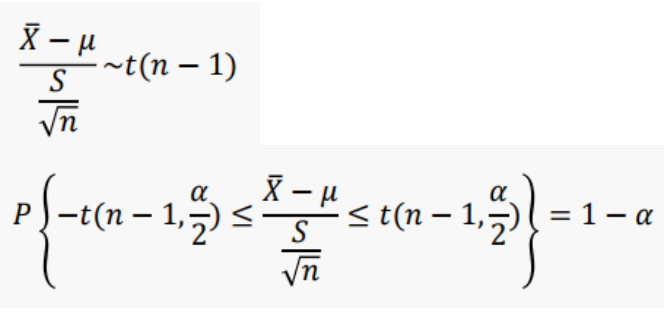
Z = X_ - E(X_)/S.D(X_)
S.D(X_) = 𝜎/√n
여기서 우리는 𝜎를 모르기 때문에, S 표본표준편차로 대체하였음.
대체를 했기 때문에 t통계량을 사용해야함.
- 표본 크기가 클 경우 Z통계량을 사용
어쨋거나, Z통계량을 써도 t 통계량을 써도 표준확률분포표, t확률분포표를 봐야함.
**두 가지 방법을 사용할 때 유념해야하는 부분이 있는데,
표준정규분포표는 P(Z ≤ z)=p
예) Z0.95 = 1.64
그래프 상으로는 뒷면적에 대한 확률을 제공한다.
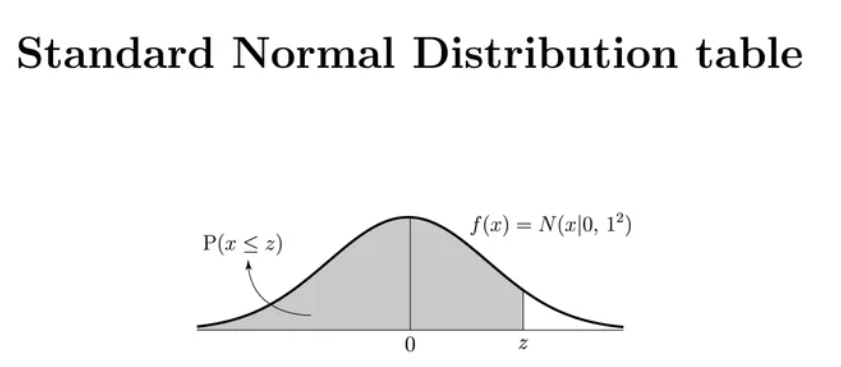
t확률분포표는 P(T≥t)=p
그래프 상으로는 앞면적에 대한 확률을 제공한다.
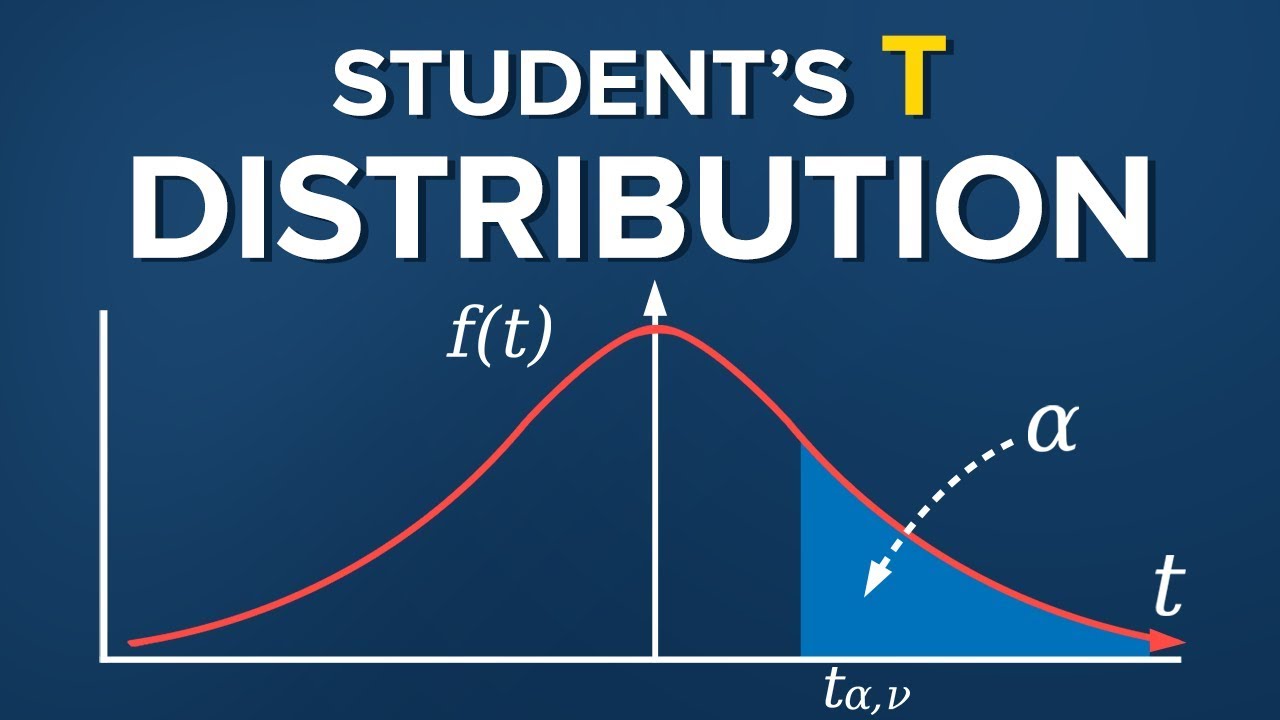
이번 강의는 통계 분석 시 많이 사용하는 통계에 그렇게 많이 나오는 유의수준, 신뢰구간, Z통계량과 t 통계량에 대해 설명해 주셨는데,
중간에 정신이 약간 혼미해졌다..후..
그래도 차근차근 설명해주시고 예제에 증명도 넣어 주셔서 복잡한 수식을 풀어가는 과정이 있다보니 한결 수월하게 이해가 되었다.
한 번만 보면 이해가 가기 어려우니 시간 날 때마다 틈틈히 봐서 내 것으로 온전히 만들어야 겠다.
이외에 매 통계 강의 뒤에 예제가 있어서 풀어볼 수 있고, 풀이도 알려주셔서 바로 적용해 볼 수 있다.
통계 기초 강의 맛보기는 유튜브에서, 강의는 메타코드M 사이트에서 들을 수 있다.
데이터 분야에서는 어떻게 쓰이는지에 대해서도 알려주셔서 이해가 쉬웠다.
https://youtu.be/r7jTwciTdXo?feature=shared
'배움' 카테고리의 다른 글
| [가벼운 학습지] 가벼운 학습지 중국어!! 도전해보자! 3주차 (0) | 2024.02.11 |
|---|---|
| [통계학] 5시간 만에 끝나는 통계학 기초강의_메타코드M_통계검정 (0) | 2024.02.10 |
| [가벼운 학습지] 가벼운 학습지 중국어!! 도전해보자! 2주차 (0) | 2024.02.04 |
| [통계학] 5시간 만에 끝나는 통계학 기초강의_메타코드M_연속확률분포 (0) | 2024.02.03 |
| [통계학] 5시간 만에 끝나는 통계학 기초강의_메타코드M_이산확률분포 (0) | 2024.01.31 |