[통계학] 5시간 만에 끝나는 통계학 기초강의_메타코드M_통계검정

통계학 기초 강의

통계 기초 이론 마지막강! 통계 검정이다.

5시간 만에 끝나는 통계 기초 이론

 

7강 통계검정은 약 30분 길이로 되어 있다.

통계검정은 내가 설정한 가설에 대해 통계적으로 타당한지 확인해볼 수 있는 중요한 장이라고 볼 수 있다.

 

6.1.1. 통계검정 : 가설

 

 

1. 가설 검정

설정한 가설이 옳을 때 표본에서의 통계량과 통계량의 분포에서 이론적으로 얻은 특정 값을 비교하여,

가설의 기각/채택 여부를 판정하는 방법

 

- 확률적 오차 범위를 넘어서면 가설을 기각한다

- 유의수준( 𝛼 ) : 기각/채택의 여부 판단기준

 

ex) 실제 통계량과 이론적 통계값을 비교하는 것.

 

 

2. 가설의 종류

1) 귀무가설 (H0)

  - 대립가설과 상반되는 가설로, 일반적인 사실을 귀무가설로 설정

  - 효과가 없다, 차이가 없다 등의 내용

 

2) 대립가설 (H1)

  - 입증하고자 하는 가설

  - 효과가 있다, 차이가 있다 등의 내용

 

6.1.2. 통계검정 : 오류

 

1. 가설설정의 오류

- 제1종 오류 (𝛼)

 : 귀무가설을 채택해야 했음에도 이를 기각할 오류

 : 표본으로부터 얻은 검정결과가 우연에 의해 잘못 판단되었을 가능성

 : 𝛼는 일반적으로 5%로 설정

예)  신약에 효과가 없음에도 있다고 판단할 오류

 

- 제2종 오류 (𝛽)

 : 귀무가설을 기각해야 했음에도 이를 채택할 오류

 : 실제로는 효과가 없는데 효과가 있다고 잘못 결론 내릴 가능성

 : 𝛽는 일반적으로 10%로 설정

예) 신약이 효과가 있었음에도 없다고 판단할 오류

 

필드에 따라 어떤 오류가 중요한지가 갈린다

 

예) 신약개발

귀무가설 : 신약이 효과가 없다

대립가설 : 신약이 효과가 있다

 

1종 오류 : 신약이 효과가 없는데(귀무가설이 맞음) 효과가 있다고 판단할 오류 : 안전성에 있어서 위험!!!!

* 신약이 효과가 없는데 있다고 판단되어 제공 - 수많은 사람들이 위험함.

 

2종 오류 : 신약이 효과가 있는데(대립가설이 맞음) 효과가 없다고 판단할 오류

* 신약이 효과가 있었는데 없다고 판단되어 다시 임상실험을 진행하거나 프로젝트가 중지

 

6.1.3. 통계검정 : 요소

 

1. 유의수준 (significance level)

- 제1종 오류( 𝛼 )를 범할 확률의 최대 허용한계

* 설정해주면 됨(일반적으로 5%)

 

2. 유의확률 (p-value)

- 검정통계량 값에 대해 귀무가설을 기각할 수 있는 최소의 유의수준으로 귀무가설이 사실일 확률

- 𝛼 > p-value : 귀무가설 기각

- 𝛼 < p-value : 귀무가설 채택

예)

유의수준 : 0.05

p-value : 0.03

-> 귀무가설을 기각

 

3. 임계값 (critical value)

- 기각역과 채택역을 나누는 경계값

- 기각역 : 귀무가설을 기각하게 되는 검정통계량의 관측값의 영역

- 채택역 : 귀무가설을 채택하게 되는 검정통계량의 관측값의 영역

- 검정통계량의 관측값이 기각역에 속하면 귀무가설 기각

 

임계값과 유의수준/유의확률로 귀무가설 채택/기각 여부를 결정할 수 있는데

 임계값의 확률 : 유의수준(면적값)

유의확률<유의수준 -> 귀무가설 기각

 

6.1.4. 통계검정 : 절차 

 

1. 검정할 가설을 설정(귀무가설, 대립가설)

  예) 신약 효과가 없다. / 내 키가 170cm 보다 같거나 작다.

 

2. 유의수준을 설정

  예) 𝛼 = 0.05

 

3. 임계치를 결정하고 검정통계량과 임계치를 비교 (혹은 유의수준과 유의확률 비교)

 

4. P-value값이 유의수준보다 작으면 귀무가설을 기각

 

6.2.1. 통계검정 : 양측검정과 단측검정

통계검정에는 양측검정과 단측검정 두 가지가 있기 때문에 확인해서 검정방법에 맞게 써야 한다.

 

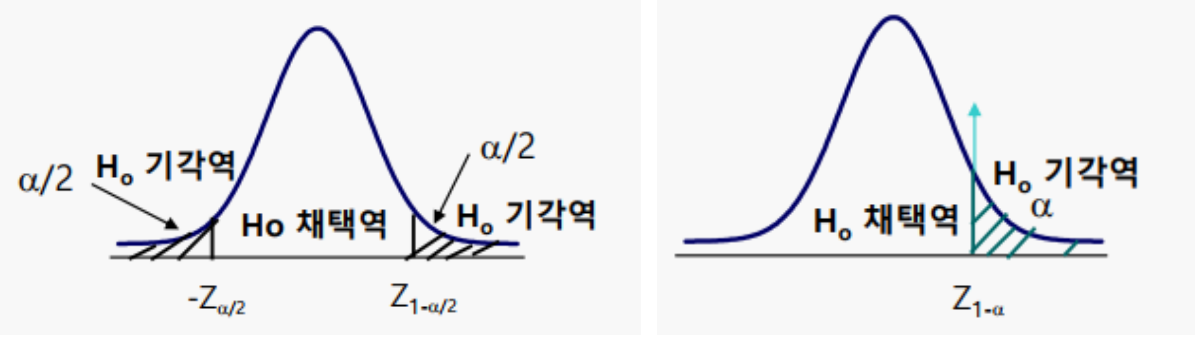
1. 양측검정 (Two-sided)

- 기각역이 각각 왼쪽과 오른쪽 두 부분으로 구성된 가설검정

- 양쪽 기각역의 합 = 유의수준

얘) 유의수준이 0.05라면 양 옆이 각각 0.025의 유의수준을 커버하는 임계값을 설정해주면 된다.

 

가설 : A와 B가 같지 않다

 

2. 단측검정 (One-sided)

- 기각역이 한쪽으로만 구성되는 가설검정

- 한쪽 기각역이 유의수준

 

가설 : A와 B보다 크거나 같다 (대소비교)

 

6.2.2. 통계검정 : 모평균 검정

 모평균을 검정하기 위해서는 크게 4가지 시나리오가 있다.

 

1. 정규모집단의 경우

  1) 모분산이 알려진 경우 : Z 검정 통계량

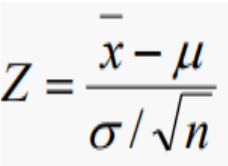
  - 모분산을 아는 케이스는 많지 않음.

 

  2) 모분산을 모르는 경우 : t 검정 통계량 (자유도 n-1)

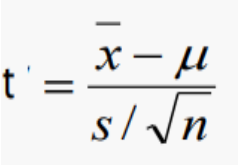
 * 표본 크기가 크지 않을 때!! 사용 

 

2. 표본 크기가 큰 임의의 모집단

  1) 모분산이 알려진 경우 : Z 검정 통계량

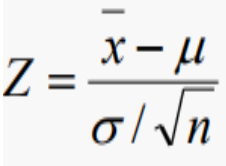
  2) 모분산을 모르는 경우 : Z 검정 통계량

 

 

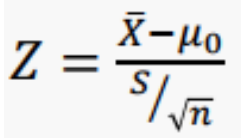
이번 강의는 가설 검정에 대한 절차와 전반적인 내용에 대해 설명해주셨다.

실험 할 때, 일반적으로 유의수준을 0.05에 맞춰서 통계 검정을 하곤 했었는데,

이게 얼마나 중요한 것인지, 그리고 모분산을 아는 경우와 모르는 경우 등에 따라 어떤 검정량을 써야하는지 알게 되어 시원했다.

---

이외에 매 통계 강의 뒤에 예제가 있어서 풀어볼 수 있고, 풀이도 알려주셔서 바로 적용해 볼 수 있다.

통계 기초 강의 맛보기는 유튜브에서, 강의는 메타코드M 사이트에서 들을 수 있다.

데이터 분야에서는 어떻게 쓰이는지에 대해서도 알려주셔서 이해가 쉬웠다.

---

https://youtu.be/r7jTwciTdXo?feature=shared

 

https://mcode.co.kr/video/list2?viewMode=view&idx=45